Geometry 几何

问题自查

1. 几何表示
   计算机中如何编码几何？
   polygon mesh表示的优劣？triangle mesh的几种表示？
   什么是细分曲面？举例两个具体算法？
   什么是网格参数化？举出具体原因的例子？举例一个具体的算法流程？
   
2. 几何处理
   离散微分几何：平均邻域(3)、法向量、梯度、拉普拉斯算子(2)？
   网格平滑，从扩散模型到Laplace处理？两种Laplace算子的效果？
   Poisson图像编辑和Laplace网格编辑的关联？条件的表达？
   网格简化的动机？流程？Lab2是怎么处理的？
   
3. 几何重建
   什么是几何重建？输入、处理、输出是什么？处理时有什么核心步骤？
   二维和三维的平移变换怎么用矩阵表示？考虑三维绕不同轴的旋转？
   复述ICP的算法思路？初始化和SVD的数学计算？
   两种几何重建的方法分别是什么？具体过程？
   model fitting的方法？如何利用采样一致性？
   
4. 几何变换

目录

• Geometry 几何
  • 08 Geometry Representation (几何表示)
    • Polygon Mesh – Triangle mesh (三角网格)
    • Subdivision Surface (细分曲面)
      • 1）Catmull-Clark Subdivision
        • 1. 新增“边点”、面心
        • 2. 更新顶点
        • 3. 将更新过的点与点相连，更新边
        • 4. 储存更新的面
      • 2）Loop subdivision
        • 1. 每条边上新增顶点
        • 2. 更新旧顶点
    • Mesh Parameterization(网格参数化)
      • 网格参数化
      • Spring System
        • 1. 能量函数
        • 2. 最优化方程
        • 3. 解线性方程
  • 09 Geometry Processing (几何处理)
    • Discrete differential geometry (离散微分几何)
      • Local Averaging Region (局部平均区域)
      • Normal Vectors (法向量)
      • Gradients (梯度)
      • Laplace-Beltrami Operator (拉普拉斯)
    • Mesh Smoothing (网格平滑)
      • 从 “扩散” 到平滑
      • 流程
      • 拉普拉斯算子的两种形式
    • Detail-Preserving Mesh Editing (网格编辑)
    • Mesh Simplification (网格简化)
      • 网格简化
      • 流程
  • 10 Geometry Reconstruction (几何重建)
    • Registration (点云注册)
      • ICP 算法
        • 1. PCA (Principle Component Analysis）初始化 R,t
          • 找到 “轴”
          • 对齐
        • 2. 通过 p’i = Rp_i + t，匹配最近点
        • 3. 距离超过阈值的点对剔除
        • 4. 建立误差函数
        • 5. 最小化误差函数（SVD 优化 R,t）
        • 6. 迭代直至收敛
    • Surface Reconstruction Algorithm (表面重建)
      • Delaunay Triangulation (德劳内三角剖分)
        • 核心思想
        • 地形建模的应用
      • Poisson Surface Reconstruction (泊松表面重建)
        • step1 构造SDF
        • step2 进行 Marching Cubes
          • 空间划分
          • 顶点编码与交点插值
          • 三角形连接查询表
          • 法向量计算
    • Model Fitting (点云的模型拟合)
      • 最小二乘法
      • RANSAC
  • 11 Transformations (几何变换)
    • 1. Translation
    • 2. 2D Rotation
    • 3. Rodrigues 旋转公式
    • 4. 3D Rotation Matrix
    • 5. 投影变换

{Notification: Just a summary of personal review, for reference only. 📩}

08 Geometry Representation (几何表示)

如何在计算机中编码几何？显式表示：点云，polygon mesh, subdivision surface ；隐式表示

Polygon Mesh – Triangle mesh (三角网格)

顶点存储为坐标三元组（x, y, z），三角形通过索引表示 ( i, j, k )

关于半边数据结构: Half-Edge Data Structures](https://jerryyin.info/geometry-processing-algorithms/half-edge/)

Polygon surface是简便表示且易于处理的表示，但是对于曲面则需要更多的面片来表示。

Subdivision Surface (细分曲面)

用于创建复杂的曲面模型,，核心思想是通过不断细分一个初始网格，使得网格逐渐变得平滑，最终生成一个贴近原模型的光滑曲面。

1）Catmull-Clark Subdivision

通常用于处理 四边形网格，每次细分增加顶点数量，并通过对顶点、面、边的更新来实现光滑效果。

算法具体流程如下，在每次迭代中：

1. 新增“边点”、面心:

对于每个面（通常四边形），添加一个新的“面点“，位置是该面上所有顶点的位置的平均值，即对于四边形面 ，面点 f 的位置为：

\[P = \frac{v_1 + v_2 + v_3 + v_4}{4}\]

对于每条边，生成一个新的“边点”, 位置计算由该边的两个顶点的平均值，再加上它相邻两个面的面点的一部分，即边点e：

\[e = \frac{v_1 + v_2 + f_1 + f_2}{4}\]

2. 更新顶点:

生成新的点后，每个原始顶点的位置会根据它周围相邻的面和边的信息进行加权平均更新，按照公式：

\[v = \frac{1}{n} \left( \frac{f_1 + f_2 + f_3 + f_4}{4} + 2\frac{m_1 + m_2 + m_3 + m_4}{4} + (n - 3) p \right)\]

期中，m是边的中心( 不是“边点”!! ), p是顶点原来的位置，n是这个顶点邻近的边/面的数量。

3. 将更新过的点与点相连，更新边:

在更新了所有顶点的位置后，下一步连接这些新顶点，形成新的网格。

4. 储存更新的面:

经过细分后，一个原始的面经过处理后会生成4个新的面，面的数将增加。每次细分后，网格的光滑度会提高，逐渐逼近一个理想的平滑曲面。

2）Loop subdivision

常用于 三角面片 的细分，算法流程如下：

1.每条边上新增顶点

$v_0$ $v_1$是一条边的两个端点，则：

如果这条边有 两个相邻面，新的顶点位置为：

\[v_{\text{new}} = \frac{3}{8} (v_0 + v_1) + \frac{1}{8} (v_2 + v_3)\]

其中$v_2$ $v_3$是相邻三角形的第三个顶点；

如果这条边只有 一个相邻面，新的顶点位置是该边的两个端点的中点：

\[v_{\text{new}} = \frac{v_0 + v_1}{2}\]

2. 更新旧顶点

更新顶点 v 的位置：

\[v' = (1 - n * u) v + \sum_{i=1}^{n} u v_i\]

其中，

• $v$ 是顶点的原始位置
• $n$ 是该顶点的度数（即相邻的面数）
• $u$ 是加权系数：$n=3$ 则 $u=\frac{3}{16}$, 否则$u=\frac{3}{8n}$
• $v_i$ 是与该顶点相邻的每个顶点

通过以上操作，每个三角形都会被细分为 四个子三角形。

Mesh Parameterization(网格参数化)

网格参数化

网格参数化是将一个三维表面（如一个三角形网格、四边形网格等）映射到 二维空间 的过程，使得每个 3D 点都能与一个 2D 坐标对 (u, v) 相对应。

应用：纹理映射，世界地图绘制(立体投影——角度不变^面积变化、墨卡托投影——无角度变形^面积变形显著、朗伯投影——保面积和角度^地图外围的区域形变会比较大)

​ 按照参数域的不同，网格参数化可以分为：(1)平面(planar)参数化，即将网格映射到平面；(2) 球面(spherical) 参数化，即将网格映射到规则的球面；(3) 基域(simplicial) 参数化，采用一个同构的简化模型作为参数域；以及基于其它参数域的参数化．

​ 按照参数化过程中保持哪种几何量，可以将参数化分为保长度 (Isometric) 的参数化、 保角度(Conformal) 的参数化、保面积 (Equiareal) 的参数化等等，即：将网格曲面映射到 平面上时，分别保证长度、角度、面积不发生扭曲．事实上，保长度的映射等价于既保角度 又保面积的映射．从三维网格表面映射到平面或其他参数域，理想的参数化是保形参数化， 即保持局部形状不发生改变．这里的形状描述包括长度、角度、面积等几何度量．但理论上只有可展曲面(developable surface) 存在保形参数化，如圆柱侧面，而一般的曲面在进行映 射时都会发生不同程度的扭曲．

​ 寻找网格表面顶点和平面上点之间的一一对应，又可以分为两种类型的平面参数化：(1) 开网格参数化，这种情形下网格是具有边界的开网格，又分为固定边界映射和自由边界映射；(2) 闭网格参数化，这种情形下网格构成一个封闭曲面，通常人为指定一条边界将封闭 网格切开，然后转化为开网格进行参数化

来源：VCL Lab - Peking University

Spring System

对于平面参数化，引入一种基础的参数化方法：Spring System——通过 最小化能量 来找到最优的网格参数化或顶点位置

1. 能量函数

定义弹簧系统的总能量函数E：

\[E = \frac{1}{2} \sum_{i=1}^{n} \sum_{j \in N_i} \frac{1}{2} D_{ij} \| \mathbf{t_i} - \mathbf{t_j} \|^2\]

其中，

• $t_i=(u_i,v_i)$ 是二维参数空间中点 $i$的坐标，$t_j$ 同理。
• $D_{ij}$ 是顶点 $i$ 和 $j$ 之间的弹簧系数。
• $N_i$ 是与顶点 $i$ 相邻的顶点集。

2. 最优化方程

为了最小化系统的总能量E，通过求解能量函数的 梯度 来优化顶点的位置，即：

\[\frac{\partial E}{\partial t_i} = \sum_{j \in N_i} D_{ij} (\mathbf{t_i} - \mathbf{t_j}) = 0\]

做简单的变换，有：

\[t_i = \sum_{j \in N_i} \lambda_{ij} t_j\]

并定义系数（coefficient)为：

\[\lambda_{ij} = \frac{D_{ij}}{\sum_{k \in N_i} D_{ik}}\]

常用的仿射组合系数有三种：平均系数、值坐标系数、 调和坐标系数

3. 解线性方程

即转化为这个线性方程：

\[t_i - \sum_{j\in N_i} \lambda_{ij} t_j = 0\]

而在网格的边界上，某些顶点的位置是已知的，固定边界映射过去，作为给定的边界条件来限制网格的参数化。

构建线性方程组 $At=b$，$A$ 是表示网格中每个顶点和相邻顶点之间关系的矩阵，$t$ 是需要计算的未知的顶点位置，$b$是已知的边界条件约束。再用如Gaussi-Sidel迭代 求解即可。

09 Geometry Processing (几何处理)

Discrete differential geometry (离散微分几何)

通过离散化技术将连续的几何概念和工具转化为离散的形式，以便计算机处理。 详细内容推导见 slides: 几何编辑、tutorial: CS 15-458/858: Discrete Differential Geometry – CARNEGIE MELLON UNIVERSITY | SPRING 2022 | TUE/THU 11:50-1:10 | GHC 4215

四个基本概念以及表示：

• Local Averaging Region (局部平均区域)

  定义三角网格顶点上的微分量

  

• Normal Vectors (法向量)

  定义三角形内部点和顶点的法向量

• Gradients (梯度)

  由顶点线性插值三角形内部点的梯度

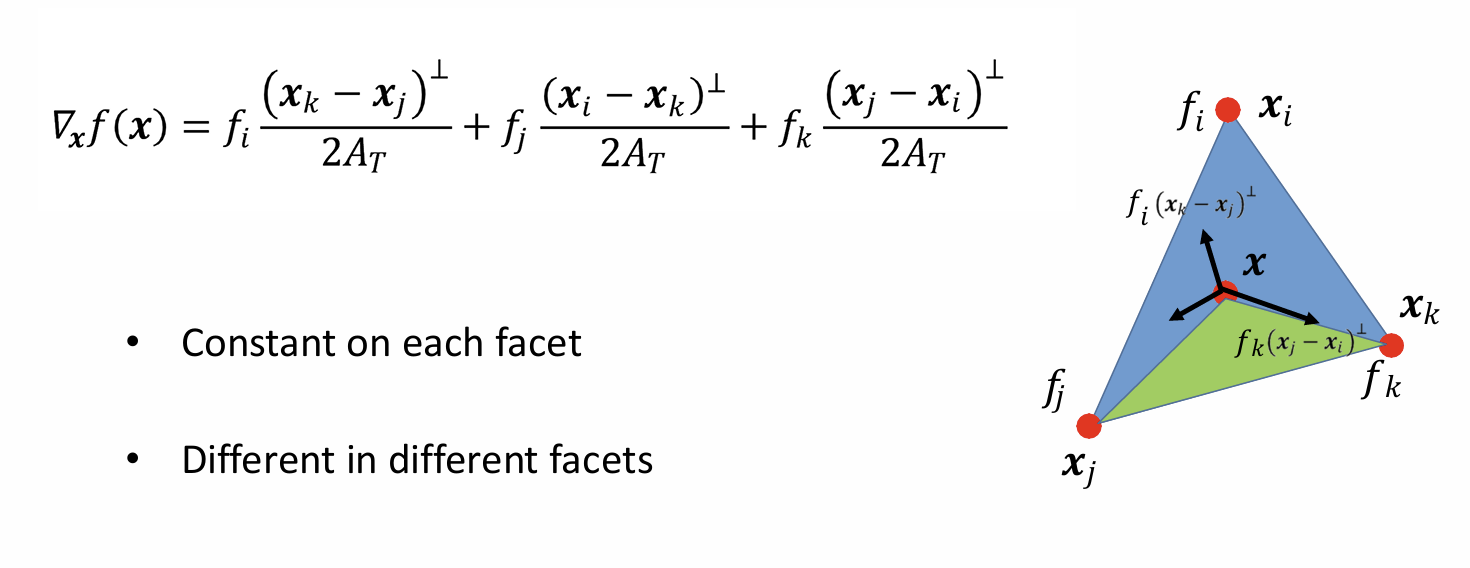
• Laplace-Beltrami Operator (拉普拉斯)

  顶点Laplace算子的一般形式，均匀、余切情况 均匀情况：$ w_{ij} = \frac{1}{N_i} $

---

在上一讲，我们已经学习了几何处理中的网格细分和参数化；接下继续学习三个不同的几何处理方法。

Mesh Smoothing (网格平滑)

从 “扩散” 到平滑

类比图像处理，平滑就是 “去噪” 的过程，改善网格的顶点分布使得其更加平滑、自然。

借助 “扩散流” 的模型来理解，对于一个时空信号 f(x,t), 扩散流公式：

\[\frac{\partial f(x,t)}{\partial t}=\lambda \Delta f(x,t)\]

应用到网格平滑上，可以吧将带噪音的顶点坐标理解成杂乱分布的热量，遂扩散的进行，热量分布逐渐趋于平衡，于是顶点构成的表面趋于平滑所以，利用定义在表面的拉普拉斯算子，这里关注 拉普拉斯平滑：修改网格顶点的位置，使得每个顶点的位置趋向其邻域的平均位置。

流程

①空间离散化，将函数值离散为网格顶点上的值，f(t) = (f(v1,t), f(v2,t),….f(vn,t)), 对每个顶点：

\[\frac{\partial f(v_i,t)}{\partial t}=\lambda \Delta f(v_i,t)\]

于是，有矩阵形式：

\[\frac {\partial \mathbf{f}(t)}{\partial t} = \lambda \cdot L\mathbf{f}(t)\]

②对于时间的离散化，采用均匀间隔的时间步长h，利用有限差分近似等式左侧的偏微分：

\[\frac {\partial \mathbf{f}(t)}{\partial t} =\frac{ \mathbf{f}(t+h) - \mathbf{f}(t)}{h}\]

显示欧拉，形式可以改写成：

\[\mathbf{f}(t+h) = \mathbf{f}(t)+h\frac {\partial \mathbf{f}(t)}{\partial t} = \mathbf{f} + h\lambda \cdot L \mathbf{f}(t)\]

即， 每经过一个h的时间步，用此式更新每个顶点上的函数值，直至达到设定的迭代停止条件。带入“网格平滑” 的背景，令函数 f 就表示顶点的坐标，则得到了第（k+1）步的 Laplacian smoothing更新公式：

\[\mathbf{x}_i^{k+1} = \mathbf{x}_i^{k}+ h \lambda \cdot \Delta\mathbf{x}_i^{k}\]

拉普拉斯算子的两种形式

①均匀算子情况下，

\[\Delta v_i = \frac{1}{|N(v_i)|} \sum_{j \in N(v_i)} (v_j - v_i)\]

只考虑邻居的数量以及邻顶点的位置信息，忽略了面的曲率等信息，因而平滑 沿重心方向 移动，即相邻点的平均位置；

②余切算子情况下，

\[\Delta v_i = \frac{1}{2A_i} \sum_{j \in N(i)} \left( \cot \theta_{ij} + \cot \theta_{ji} \right) (v_j - v_i)\]

考虑了每个顶点相邻三角形的几何特性（邻接边的角度），够使顶点沿着网格的几何结构进行移动，更能够保留几何特征。

---

Detail-Preserving Mesh Editing (网格编辑)

操纵和修改网格表面的几何形状，同时能够保留原始网格几何细节的操作。

回顾：泊松图像编辑，类比到三维的应用即 拉普拉斯网格编辑。

目标：指定一些顶点的目标位置后，重建一个既满足这些顶点约束、又尽可能保持局部拉普拉斯微分坐标的网格。数学公式：

\[\arg \min_{v'_1, \dots, v'_n} \sum_{i=1}^n \left\| L(v'_i) - \Delta_i \right\|^2 + \sum_{j \in C} \left\| v'_j - u_j \right\|^2\]

其中：

• $v’_i$ 是顶点 $i$ 的新位置。
• $L(v’_i) $是拉普拉斯算子作用于顶点 $v’_i$，表示每个顶点相对于其邻居的偏移量。
• $\Delta i$ 是目标拉普拉斯误差, 原始网格或参考网格的拉普拉斯算子值。
• $C $是需要满足约束的顶点集合（边界顶点）。
• $u_j$ 是约束条件下顶点 $j$ 的目标位置。

这是一个标准的最小二乘问题，转化为线性系统迭代求解即可。

应用：涂层迁移、表面移植等。

---

Mesh Simplification (网格简化)

网格简化

为什么需要简化？

用plygon mesh来表示物体模型，但处理的物体模型通常由很多块面片组成，逐一处理渲染在游戏、可视化等场景十分影响效率；同时，并非每时每刻都需要用最高精度的模型，比如模型在远处时，本身细节就不用很精致，精度较低不影响渲染质量。所以，可以用更多的面片来表示近处物体，较少的面片来表示远处物体。

这就是网格简化：用更少的面片数来表达原有模型。

流程

为了删除多余的顶点、边和面，可以通过移除顶点、边坍塌、半边坍塌来实现；但是在坍塌边的时候需要注意，防止坍缩某条边后对模型造成较大影响 (如干扰拓扑结构），于是引入一种误差度量，计算坍塌一条边的损失，比如可以采用最基本的 Quadric Error Metrics (二次误差度量)。

详细参考 Lab2 Task3

参考资料：Surface simplification using quadric error metrics

10 Geometry Reconstruction (几何重建)

输入数据：真实世界获得的数据，如雷达扫描、RBG-D深度相机的数据，通常转化表示为点云。

目的：将输入转化为后续可以编辑的几何对象；即获取点云后，进行对齐、表面重建、模式识别拟合（通常利用RANSAC）

Registration (点云注册)

将两套点云对齐（注册）–> 找到一个正确的变换

ICP 算法

根据两组点云之间的形状匹配关系，计算出它们之间的相对变换，最大程度对齐两个点云。

具体流程如下：

1. PCA (Principle Component Analysis）初始化 R,t

主成分分析:找到互相垂直的 “基” （一组正交的轴），每一个新的轴是一个主成分，表示数据中方差大、“最重要” 的方向。

找到 “轴”

step 1.中心化数据，去均值化处理使得数据的均值为0

step 2.建立协方差矩阵 M

step 3.对协方差矩阵对角化

对于二维数据， 的两个特征向量表示数据的两条轴线：对应最大特征值的那个特征向量表示，数据在这个方向上的分布最分散（数值变化最大）；对应最小特征值的那个特征向量表示，数据在这个方向上的分布最集中（数值变化最小），对于三维数据同理。

对齐

对于两个点云S,T，中心为 $c_S,c_T$:

首先将 $c_S$ 平移到 $c_T$，则S点云中的一个点 $p_i$ 就变成了 $p_i^* = p_i +(c_T -c_S)$； 然后找到一个旋转矩阵 $R$，使得源点云通过旋转后的点与目标点云对齐,旋转后的点 $p_i’ = c_T + R \cdot (p_i^* - c_T)$；

合并，即最终源点云的点 $p_i’$ 经过平移和旋转的公式为 $p_i’ = c_T + R \cdot (p_i - c_S)$

于是，就可以找到一组初始的$R_0，t$：

\[R_0= R\\ t_0 = c_T - R \cdot c_S\]

2. 通过 $p_i’ = Rp_i + t$ ，匹配 $p_i$ 在另一个点云中的最近点 $q_i$

3. 对于匹配上的点对，距离超过阈值的扔掉

4.建立误差函数：$E=\sum |Rp_i + t -q_i|^2$

5.最小化误差函数，利用SVD分解 优化R, t

6. 迭代2-5步至误差函数足够小

---

Surface Reconstruction Algorithm (表面重建)

指点云网格化的过程，也称 Meshing

why？点云模型占用很大储存空白键；编辑调整模型较难；且放大模型后点云会变得稀疏，在物体表面露出缝隙

Delaunay Triangulation (德劳内三角剖分)

Voronoi diagram: 给定一个点集 $P = {p_1, p_2, \dots, p_n}$ 在平面（或更高维空间）中，Voronoi图是将空间划分为若干个区域，使得每个区域包含一个生成点 $p_i$，并且区域内的每个点到 $p_i$ 的距离都比到其他点 $p_j$ 的距离近。具体地，Voronoi单元是由一组点围成的区域，每个单元包含一个种子点 $p_i$，并且该区域内的任何点到 $p_i$ 的距离最小。

对于给定的一组点，找到一种“合理”的三角剖分办法。直观上，尽量不要生成狭长形状的三角形，即德劳内剖分的思想：找到一种方法 最大化所有三角形中最小的角（2D情况下，：生成结果中，任何三角形的外接圆内，都不包含任何点）

核心思想

最大化所有三角形中最小的角，于是有以下规律：

规律：任何一对存在公用边的三角形，必须满足对顶点角度的和小于180度，否则不满足德劳内三角剖分的性质（此时进行边翻转，如下：）

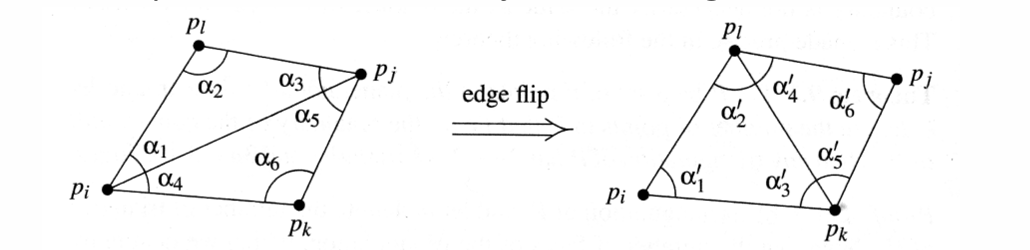
于是，由这个思路，构造如下的简易算法：

1. 初始时随意构造三角剖分
2. 逐个检查共边三角形，是否满足性质，不满足则边翻转重新连接边
3. 重复检查，直至全体满足

但是，这个算法并不高效（O(n^2)）

另外，一个有关德劳内的应用：地形建模

假设有一组二维空间中的数据点 $A \subset \mathbb{R}^2$，这些点可能代表一个地形的离散采样点。每个点 $p_i \in A$ 都有一个定义好的高度值 $f(p)$，表示该点的高度。问题：如何估算不在 $A$ 中的点的高度？

插值方法：线性插值

• 第一步：使用Delaunay三角剖分将点集 $A$ 分割为若干个三角形，通过这些三角形的边界来描述空间。
• 第二步：通过Delaunay三角剖分后的三角形，可以进行插值，计算不在 $A$ 中的点的高度。通常，通过每个三角形的顶点来进行线性插值确定其他点的高度。

Delauny in 3D

在三维空间中，有一组点集 $A \subset \mathbb{R}^3$，每个点 $p \in A$ 可能会有一些属性（如颜色、纹理坐标、深度等）问题：如何估算不在 $A$ 中的点的属性？例如，有一个稀疏的点云，并且希望得到一个连续的属性值（比如深度值）。

插值方法：双线性插值

• 使用三维Delaunay三角剖分来进行插值。三维Delaunay三角剖分将点云划分为若干个四面体，这些四面体为后续的插值计算提供了结构。
• 通过这些四面体，我们可以对不在点集 $A$ 中的点进行属性插值。插值方法可以根据四面体的各个顶点的属性值来推算其他位置点的属性。

Delaunay三角剖分保证了局部最优的连通性，使得点云的插值更加平滑和自然；而且它可以有效地避免一些不良的三角形或四面体，确保插值结果稳定。

Poisson Surface Reconstruction (泊松表面重建)

发现，上述三角剖分在输入的点云数据中包含噪声或错误的点集时，由于三角剖分必然会构造以噪点和错误点为顶点的三角形，会导致一些视觉上的异常。

而泊松表面重建则不直接构造，先构建符号距离函数隐式表达，再通过marching cubes从SDF提取三角形。

step1 构造SDF

输入：每个点 带有法向量 的点云

符号说明：对于一个空间中的实体 M，指示函数 $\chi_M$ 标识其表面 $\partial M$，在M内函数值为1否则为0；则$∇χ_M $只在 $\partial M$ 上具有非零梯度, 且表面上某点的梯度方向与该点的法向量反向。

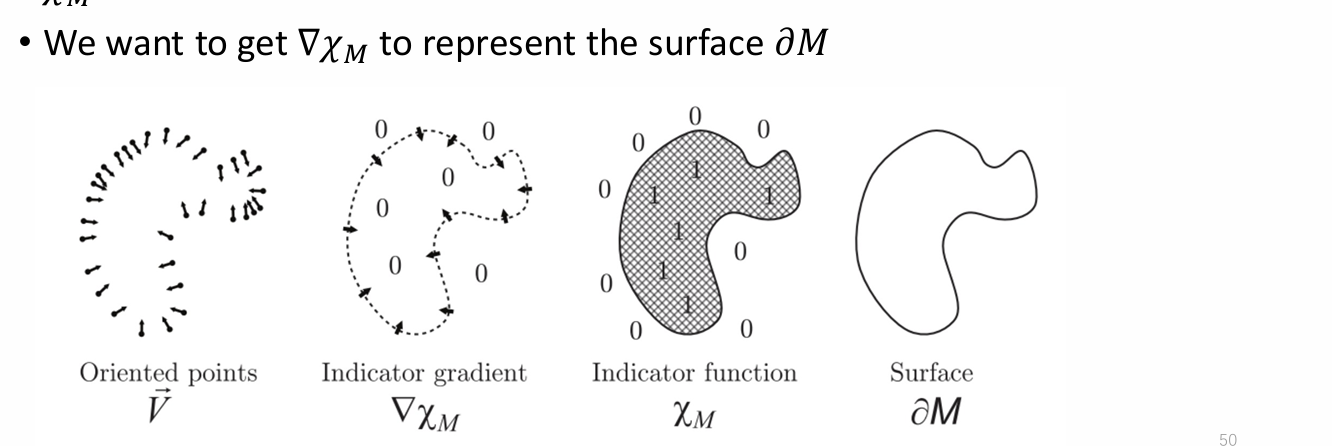
解决问题：已知函数的梯度场，还原这个函数。即根据 $ \nabla \chi_M = \mathbf{V}$ 估计 $\chi_M$

右边向量不一定可积，*通过泊松方程转化为可以估计的最小二乘解形式*：$ \Delta \chi_M=\nabla \cdot \mathbf{V}$

step2 进行Marching Cubes

目标是根据输入的隐式SDF重建三角表面

1. 空间划分

把三维空间划分成多个体素，每个立方体的 8 个顶点都有一个 SDF 值：SDF < 0 → 点在对象内部；SDF ≥ 0 → 点在对象外部。

2. 顶点编码

每个立方体的 8 个顶点可以用 0 / 1 表示 inside / outside，一共 2^8=256 种组合。用一个 8-bit 的二进制数 来编码；通过对称性这些情况可以简化为 15 种基本拓扑模式：

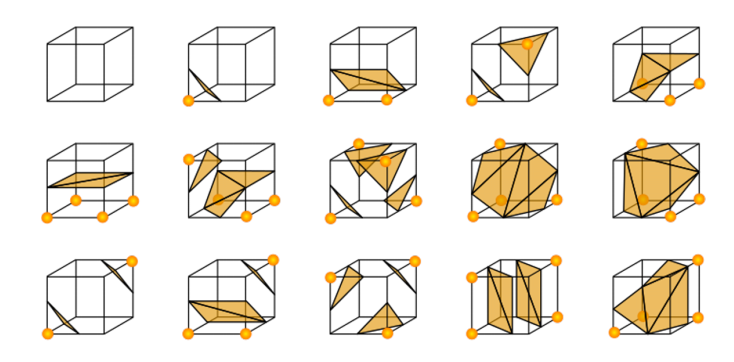
3. 变状态查询表

算法维护了==两个查询表==：

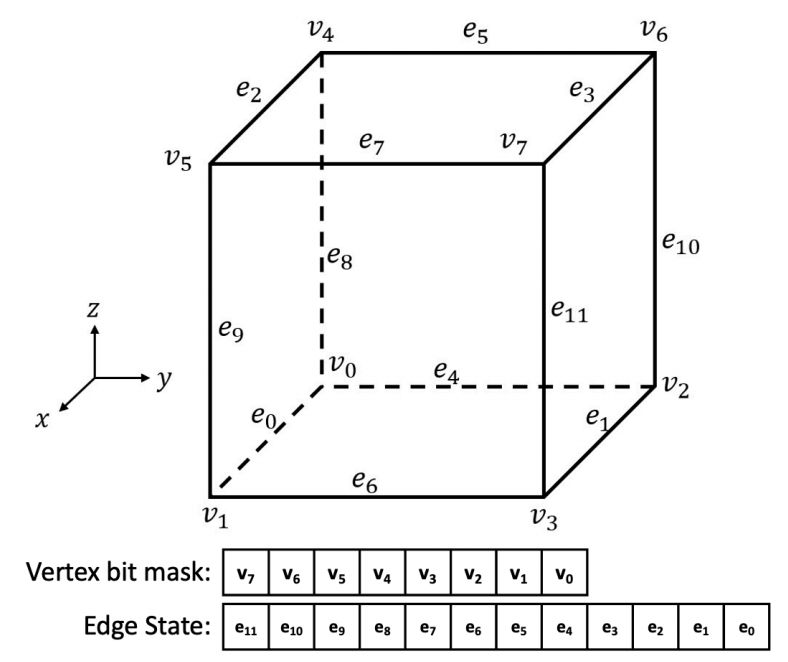
第一个表根据顶点编码成的索引查询关于边状态的编码：每个立方体有 12 条边，根据顶点 inside/outside 状态判断哪些边会被等值面穿过，用一个 12-bit 的二进制串 表示边状态。

如果某条边被穿过，就在边上生成一个交点，位置通过线性插值计算：

\[p^*=\frac{v_2-v^*}{v_2-v_1}p_1 + \frac{v^*-v_1}{v_2-v_1}p_2\]

$p_1, p_2$是边的两个端点坐标，$v_1, v_2$为端点的 SDF 值, $v^*$是等值面阈值（通常取 0）

4. 三角形连接查询表

第二个查询表包含关于这些生成的 *网格顶点之间如何连接* 的信息, 根据查表结果把交点连起来，形成面片。

5. 法向量计算

得到交点的法向量，同样由边两端的法向量插值得到; 顶点法向量直接由 SDF 的梯度计算：

\[\nabla f(x,y,z) \approx \big(f(x+1,y,z)-f(x-1,y,z),\; f(x,y+1,z)-f(x,y-1,z),\; f(x,y,z+1)-f(x,y,z-1)\big)\]

然后归一化得到。（这里法向量就是后续三角mesh顶点的法向量，会在之后处理用于光照计算等渲染的环节）

6. 输出

最终输出：网格顶点坐标、顶点法向量、三角形面片连接关系。这些数据构成了一个标准的三角形网格，可以直接用于渲染。

11-geometry-reconstruction-notes.pdf

---

Model Fitting (点云的模型拟合)

从给定的点云中提取出平面或 球体、圆柱体等几何基元的过程

最小二乘法

假设点云大致分布在某个几何模型上，然后定义一个误差函数来度量点到模型的距离，再通过最小化所有点的误差平方和来得到最优的模型参数。

解决：SVD奇异值分解

但是对离群点很敏感：如果点云里有很多噪声或异常点，拟合结果会被严重影响。

RANSAC

从点云里随机选取少量点，拟合一个候选模型，然后统计有多少点符合这个模型（即点到模型的距离小于某个阈值），记为内点；重复多次，最后选择内点最多的模型作为结果。

保证使点云里有很多噪声或离群点，它们也不会影响最终的拟合，因为只有大多数点支持的模型才会被选中。因此RANSAC在噪声环境下效果更好，但是计算量比最小二乘法大。

11 Transformations (几何变换)

1. Translation

在二维空间中，平移操作就是将一个点按照固定的距离进行平移。假设原始点的坐标为 $(x, y)$，我们希望将其平移一个量 $(t_x, t_y)$，则平移后的新坐标 $(x’, y’)$ 可以通过以下公式表示：

\[\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} t_x \\ t_y \end{pmatrix} + \begin{pmatrix} x \\ y \end{pmatrix}\]

其中：

• $x’$ 和 $y’$ 是平移后的新坐标。
• $t_x$ 和 $t_y$ 分别是沿 $x$ 和 $y$ 方向的平移距离。

2. 2D Rotation

在二维空间中，旋转操作是通过旋转矩阵将一个点围绕原点旋转一定的角度 $\theta$ 来实现的。旋转后的新坐标 $(x’, y’)$ 可以通过以下公式来计算：

\[\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\]

其中：

• $\theta$ 是旋转角度。
• $x’, y’$ 是旋转后的新坐标。

3.Rodrigues 旋转公式：

假设向量 v 是要旋转的原始向量，单位向量 k 是旋转轴的方向。θ 是旋转角度（单位是弧度）那么旋转后的向量 v’ ：

\[\mathbf{v'} = \mathbf{v} \cos\theta + (\mathbf{k} \times \mathbf{v}) \sin\theta + \mathbf{k} (\mathbf{k} \cdot \mathbf{v})(1 - \cos\theta)\]

4. 3D Rotation Matrix

在三维空间中，旋转操作需要使用旋转矩阵 $R$，这个矩阵是一个 $3 \times 3$ 的矩阵，描述了围绕某个轴进行旋转的操作。旋转矩阵作用于一个点 $p = (p_x, p_y, p_z)$ 后，点的新的坐标 $p’ = (p_x’, p_y’, p_z’)$ 由以下公式给出：

\[\mathbf{p}' = R \mathbf{p} = \begin{pmatrix} r_{x0} & r_{y0} & r_{z0} \\ r_{x1} & r_{y1} & r_{z1} \\ r_{x2} & r_{y2} & r_{z2} \end{pmatrix} \begin{pmatrix} p_x \\ p_y \\ p_z \end{pmatrix}\]

其中：

• $r_{x0}, r_{y0}, r_{z0}$，等是旋转矩阵的元素，它们描述了旋转后的新坐标轴的方向。
• $p_x, p_y, p_z$ 是原始点的坐标。
• $\mathbf{p}’$ 是旋转后的新坐标。

旋转矩阵 $R$ 具有 正交性，即 $R^{-1} = R^T$ 绕 x、y、z 轴分别旋转的旋转矩阵分别为：

\[R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(\theta) & -\sin(\theta) \\ 0 & \sin(\theta) & \cos(\theta) \end{pmatrix} \\ \\ R_y(\theta) = \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} \\ \\R_z(\theta) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix}\]

如果要绕三维空间中的任意轴进行旋转，旋转矩阵可以表示为：

\[R_{\alpha, \phi} = \begin{pmatrix} c + (1 - c) a_x^2 & (1 - c) a_x a_y - s a_z & (1 - c) a_x a_z + s a_y \\ (1 - c) a_x a_y + s a_z & c + (1 - c) a_y^2 & (1 - c) a_y a_z - s a_x \\ (1 - c) a_x a_z - s a_y & (1 - c) a_y a_z + s a_x & c + (1 - c) a_z^2 \end{pmatrix}\]

其中：

• $a_x, a_y, a_z$ 是旋转轴的单位向量，表示旋转轴的方向。
• $\phi$ 是旋转角度。
• $c = \cos(\phi)$ 和 $s = \sin(\phi)$ 分别是旋转角度的余弦和正弦。

这个旋转矩阵可以绕任意轴进行旋转而不仅仅是绕标准坐标轴进行。

5. 投影变换